「因果推論の科学」
以前「モンティホール問題」という話題を取り上げまして
[モンティホール問題なんてない] >>
そこでは 一見パラドックスに見えるこの問題も「文章読解問題としてこの様に理解されます」という私なりの感想を述べさせていただいております。
ここで大まかな内容を再掲いたしますと
--- [ 通常の書き方 ] ------------
3つのドアがあり どれか1つにお宝が隠れていて 2つはハズレです。
とりあえずあてずっぽうで1つのドアを選んでください。
次に司会者が あなたの選ばなかった2つのうち お宝がない方を開けます。
ご覧の通り空ですね。 残るドアは2つ。
さてここであなたに 選び直すチャンスをあげます。
最初の選択を変えますか? それとも変えませんか?
-------------------------
答えは「変えた方がいい」なのです。
変えないよりも変えた方が当たる確率が ”倍” になります。
こう言われると確かに ホンマかいな的な感じがしますね。
ところが こちらはどうでしょう・・
--- [ 言い直したバージョン ] -------
3個のガシャポンカプセルがあります。中は見えません。
3個のうち1個にだけお宝フィギュアが入っていて 残りはハズレです。
この3個を 1個と2個のふた「組」に分けてください。
次にどちらかの 「組」 を選んでください。
一方は1個もう一方は2個をゲットできるということです。
さて あなたはどっちの 「組」 を選びますか?
-------------------------
当然2個の方を選びますよね。
こう言われると 当たり前すぎる当たり前です。
そして この二つのバージョンの文章が論理的には全く同一であるという事を
こちら>> で述べさせていただいたのでした。
===
私はこの段階で安心して「この問題はこれで解決。これ以上掘っても何も出ん」と思っていた。 甘い!甘いぞっ!
もっと根本的な問題:
「 ではなぜ人間は この様な言い方に対しパラドックスを感じてしまうのか?
脳細胞の配線のどこに この様な認知バイアスを生んでしまう回路が潜んでいるのか? 」
そもそも論である。 よっぽど大問題である。
そして 「因果推論」 は以下の様な説明を用意します。
------------------------
ノードX[私の選択したドア]
ノードY[宝のあるドア]
ノードZ[司会者の選択するドア]
は典型的な”コライダー”を構成するので
Zを条件付けするとXとYは”擬似相関”を持ちランダムな関係ではなくなる。
人間の脳は”擬似相関”を見落とすアホの子なので これをパラドックスだと思ってしまう。
------------------------

「因果推論の科学」
ジューディア・パール/ダナ・マッケンジー
こちらが去年末から話題となり 私も今年初めに手に取り 事の重大さのあまり他の読みかけ本をうっちゃってとにかくまずはこれを読みました。*1)
===
そして 最近読んだ面白い本紹介的な感じで 軽い気持ちで何か書こうとしていたのですが(今思えばこの段階での私の理解は表面的でいい加減なものであった やめといてよかった・・)
みなさんご存知 ChatGPT騒動が勃発。世の中「AI!AI!」となってしまった。
このお祭りの中 このタイミングで
「ビッグデータ統計とか大規模言語モデルとかには因果推論が組み込まれていない。 その限りにおいてまだまだ知能とは呼べない ひよっこである!」
みたいなことを素人が言い出すのはあまりにも恥ずかしく 時代に乗り遅れ感半端なく ダサい判定されること不可避 急に自信がなくなってしまった。
ので 感想文は中止 趣味の読書として教科書をちまちま匍匐前進するなどしておりました。
ChatGPT祭り・・こういったパーリーは今までにも何度も何度もありました。
そして2023ももう中場 祭りもそろそろ落ち着いてきましたかね。
まだしばらく続く感じすか それともそろそろお開きが近い様な感じ? どうでしょうか。
なので 参ります。
===
[ 書き終わって・・ ]
ここに戻ってきてこんなこと言うのもなんですが・・
私は単なる一読者であり 専門的な事をこまごま語る立場にない事はわきまえており 今回は簡単な読書感想文として「よかったら読んでみてね」的に書いていくつもりでしたのですが・・ 長い。すいません。 うまくまとめることができない。ばさばさと削ったのですが。 流し読みするのすらめんどくさいであろうと思われ。 ですので 表面だけでも雰囲気だけでも汲み取っていただけたらそれだけでしあわせです。
=================================
ビックデータ解析の統計科学。 ちょっと古いですが
”AIひろし” である。
2017.7.22 NHK「AIに聞いて見た どうすんのよニッポン」
NHK独自開発のビッグデータ解析システム”AIひろし”で 700万データの統計分析を行ったということで さまざまな面白い結果が紹介された。
「がん患者を減らしたければ 病院数(病床数)を減らせ」
(バナナの売上とも連動しているのが面白かった)
「少子化を食い止めるには 結婚よりもクルマを買え」
(婚姻件数の増加で出生率がかえって下がる?というのが面白かった)
さて 文中の「ければ」「ためには」が気になるところである。
言い方の中に因果関係のニュアンスを滑り込ませている。
これは実は 統計科学的には反則である。
「がん患者数と病床数には 相関が見られる」
「少子化傾向と車の購入数には 相関が見られる」
と言いなさいと先生から注意される・・かもしれない。 *2)
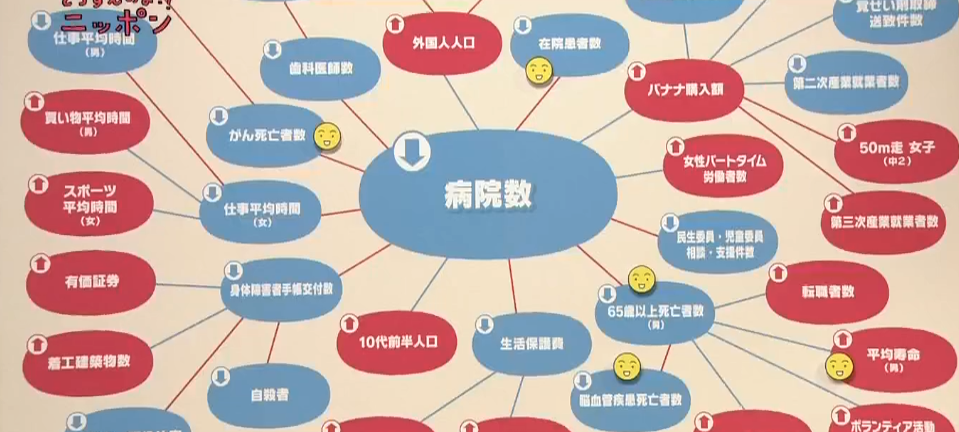
この様なグラフィックは ビッグデータの説明でよく目にする。
各ノード:球体はたくさんの線で結ばれ 球体の大小・線の太さでデータの大きさや相関関係の強さを表現し 多数のノード同志の結びつき方を一望できる。
そしてこのグラフィックには「原因と結果」という概念は表現されていない。
統計科学ではそう言う解釈を加えてはいけない。
何と何がどれだけ相関しているか について述べるのみである。
=================================
”統計的因果推論”とは 統計科学の新しい勢力。
統計科学は たくさんのデータを取り 物事同士の相関関係を炙り出していく技術。
そして伝統的な統計科学では いの一番に「相関関係と因果関係の混同」が厳しく注意される。
有名な例え話ですが
アイスクリームの売上 と 犯罪発生率
というデータが集まったとする。 分析してみると
アイスクリームの売上が高い時は 犯罪発生率が高く
アイスクリームが売れにくい時は 犯罪発生率が低かった。
このデータから
相関関係:「アイスクリームの売上と 犯罪発生率は ”相関”する」
が判明する。
しかし
因果関係:「アイスクリームの売上が 犯罪の”原因”である」
あるいは 「犯罪が アイスクリームの売上の”原因”である」
は常識的に考えておそらく間違いであろう。
統計データはあくまで”相関関係”を語る。 ”因果関係”は語らない。「この鉄則を肝に銘じたまえ!」
古典的な統計学の世界では 因果関係の概念は排除されてきた。
それどころか 原理主義的な頑固さで 因果関係について語ることを禁じる 語るも穢らわしい事として忌避するまである。
しかし 世界の実際として 因果関係は確かに存在しそうな気がする。
先の例では 気温 という要素が見落とされていた可能性がある。
気温のデータをシステムに追加すると
相関関係として3つのデータが連動して増減するトライアングルが描ける。
一方 因果を推論することが許可されれば
「アイスと犯罪の共通の原因が気温である」という ”有向グラフ” が書ける。
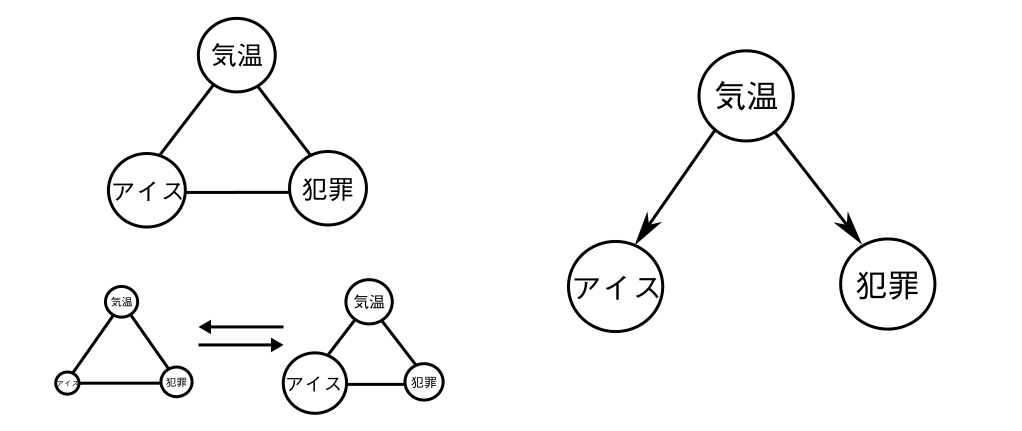
左図は データ間に相関があると言っているにすぎない
例えば「Bの値が増加した時にAとCの値も増加しているというデータが取れた」と言っている。
右図は 因果関係を表す有向グラフ
「親ノードの増減を原因として その結果子ノードの値が増減する」という仮説を打ち出している。(”フォーク”と呼ばれる因果関係になっている)
===
気圧計の値/台風の勢力 の例
統計データは
気圧計の読み取りデータ と 台風の勢力のデータ
両者の間に相関関係があることを示すだろう。 *3)
有向グラフを当てずっぽうに書いてみる・・
気圧計の値 → 台風の勢力

気圧計のつまみを調整することにより台風を生成できると言っている。
「 こんな因果関係は馬鹿馬鹿しい 矢印なんか引くからいけないのだ 相関を示す線だけ引け、線だけ。」
気圧計の値--台風の勢力
これに対し統計的因果推論派は「いやいや 正しいと思われる方向に矢印を書きモデル構築しようぜ」と言う。
台風の勢力 → 気圧計の値
これは正しそうに見える。このモデルで進めてみようよ。
===
因果関係に関する話題の中でも タバコ論争 はとりわけ目立つ話題である。
喫煙は癌の”原因”なのか”相関”なのか?
タバコメーカーは ”遺伝的傾向”という測定不能な交絡因子を持ち出し 議論をデータ解釈の沼に引き摺り込む。
データをこねくり回し わかった様なわからない様なデータ解釈で煙に巻き逃げ切ろうとする。
統計科学としては 得られたビッグデータからは 物事の相関についてしか上手く語れず
喫煙と癌 遺伝的傾向と癌 さまざまな因子の因果関係・影響力の重み付けについて上手く総括できなかった(現在ではほぼ解決してますが)。
因果推論からの提案は 因果関係を明確にしたモデルを仮定し 実際のデータと比較しモデルの妥当性を確かめ 喫煙→癌 の因果経路の強さを導くことである。
さらに強力なことに この例の様な測定不能な交絡因子 ”遺伝的影響” がある場合も 論理的解決方法があり
喫煙→癌 経路上に「タールの沈着量」という”フロントドア”なるものをセットしデータを収集し 喫煙とタールの2つのノードに対し調整(重み付け足し上げ)することで 喫煙→タール→癌 というルートに対して正しい評価を導き出す という理論体系を 「因果推論」は作り上げている(タール沈着は遺伝子には影響されないであろうことが効いてくるのだ)。
この操作によって
遺伝的原因→癌 の経路よりも
喫煙→タール→癌 の経路の方が重いことが 論理的に導かれる。
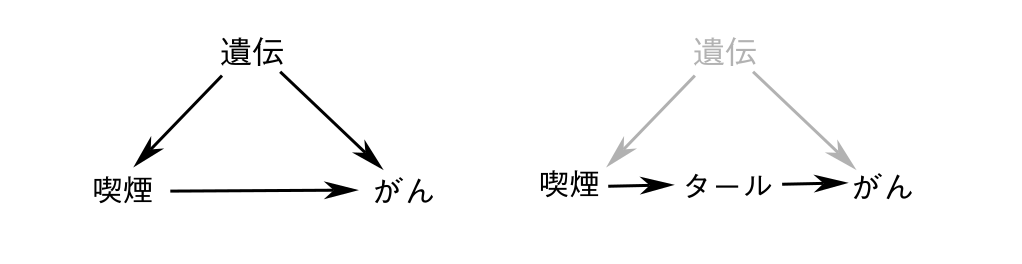
このタバコ問題の様な問題は世の中に溢れている。
「性差別意識がxx大学への入学のバイアスとなっているか?」
「この治療法は この薬は効くのか 害はあるのかないのか?」
こういった因果関係問題たちに対し 統計因果推論は 論理的な解法を提案しているのである。
===
考えるに・・
わしら人間は 因果関係を常に問うている存在なんである。
人間の意識は 物事の因果関係を知りたくてたまらない。
何が一番悪いのか 誰のせいなのか 知りたい決めたい。
どうすれば将来この問題を避けられるのか考えたい。
そういう意味において 因果関係の分析能力が備わって初めて AIは人間に近づくことができるはずだという事になる。
ビッグデータの統計解析・大規模言語モデルだけでは人間にはなれないということだ。
「はやく人間になりた〜い」
「もう少し我慢しなさい すぐそこですよ」
因果推論の体系は もろにプログラミング可能な仕組みである。 明日にでも因果推論モデルはAIに実装可能。
そして 組み立てたモデルに対し修正フィードバックを繰り返して精度を向上させていくという仕事は まさにAIの真骨頂である。
最終的には 人間が推論でミスしがちなパラドックスを論理的にすいすい回避していく知能を獲得するかもしれない。
その時初めて AIは人間を超えるのかもしれない。
=================================
さて ここまでの例はノードが少ない簡単なものばかりでした。
でも現実の世界は こんな単純なグラフで表されはしないんではないか?
多くのノードが存在し多くの経路によって原因と結果の巨大ネットワークが作られていると思われるのだが。
そして我々が知りたいのは この巨大マップの中のピンポイント:ノードXを原因としてノードYを引き起こす因果関係の強度はいかほどか だったりする。
そんな分析が本当にできるのか?
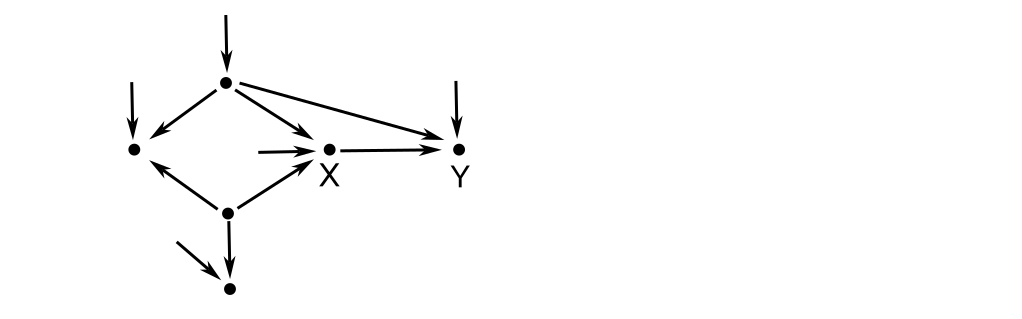
教科書に出ていたダイアグラムの例
たとえばこんなグラフでも 因果推論では パズルを解く様に手順を踏んで読み解いていくことができる。
実は 全てのグラフはとどのつまり 以下のたった3つのパターンを部品として構成できる。 素因数分解できる 原子に還元できる。
なんですと? このような事を聞くと理系オタクの血はとたんに騒ぎはじめる!「その話詳しく。」
チェーン (媒介、 連鎖)
フォーク (交絡、 分岐)
コライダー (合流)
(教科書によって言い方がいろいろ)
統計的因果推論は どんな大きなグラフもこれら3つの要素に分解できると言っている(この事自体は前段階であるベイジアンネットワーク理論が起源)。
マップをこれらの要素に分解しパズルを解く。
大まかな流れはこんな感じ:
XからYへ直接情報が流れる経路に注目し 間接的な経路は”ブロック”していく。
チェーン・フォーク・コライダーを読み解く事によって 流れの交通整理やブロック方法は機械的に導かれます。
(色々な手法があるようですが 例えば”バックドア基準”なるものを満たすノードを発見し そこへつながるパスを切断し ノードに対し”調整”を行う)
こうして 新たに改修された回路ができあがると これに基づき統計科学の流儀の方程式が得られる。
Xのパラメーターに”介入”を行って(例えばX=0:薬を投与しない/X=1:薬を投与する を強制代入する) Y(例えば健康が回復するかしないか) を得る。
これで 薬投与の有無が患者の回復に統計的意味のある差を生じているかどうか が導き出される。
===
三つの元素について
[ チェーン ]

X→Y→Z
風・・桶屋 的な因果関係である。
これについてはとりあえず難しい事は何もなさそうである。
(実はそうでもないのだが きりがなくなっていくので・・)
===
[ フォーク ]
前に紹介した「気温・アイス・犯罪」系はフォークである
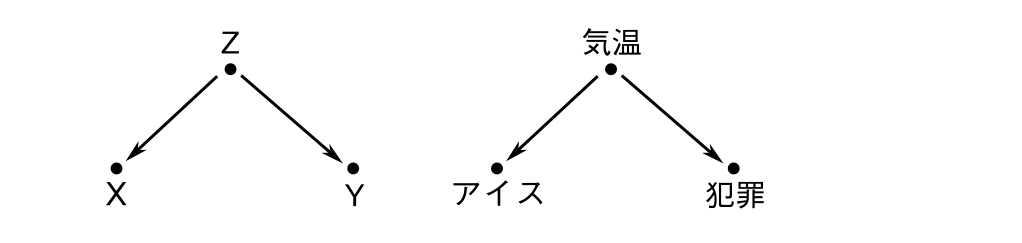
X←Z→Y
このダイアグラムは「気温という要素が アイスと犯罪の共通の原因(共通の親:交絡因子)として この様な因果関係を構成している」という仮説を表現する。
アイスと犯罪は直接因果関係では結ばれていないが 気温に連動した”擬似相関”をとる。
フォークでは 気温 を”条件付け”しない限りにおいて アイス・犯罪は 従属する開通した回路として動作する。
親ノードの変化が 2つの子ノードの値を同時に変化させる 2つのノードが一体となって動作する様な形で パス的には左右が接続した状態になるわけです。
しかし 親の値を”条件付け”する:値を固定すると 2つの子ノードの値はスタックするつまり アイス・犯罪 の間の同期動作の情報の流れが止まる ブロックされる。

年齢 身長 学力
これもフォーク
身長と学力の間に直接の因果関係はもちろんない(整形手術しても頭は良くならん)のであるが 年齢を交絡因子として統計的相関が観察されるであろう。
身長が高ければ たぶん学力も年相応に高いという事である。
ところが 年齢をたとえば17歳という条件付けすると 身長も学力も17歳なりの値の範囲に限定され その中では背が高い子が学力も高いなんて事は非科学的な話になる 相関は消えるのである。
===
[ シンプソンのパラドックス ]
フォークについての話題の中で興味深いのが「シンプソンのパラドックス」である。
こちらは フォークの流れをブロックすることで因果関係を見極める と言う話になっている。
| 薬投与 | 薬投与なし | |
|---|---|---|
| 男性 | 回復93% 81/87 (人) | 回復87% 234/270 (人) |
| 女性 | 回復73% 192/263 (人) | 回復69% 55/80 (人) |
| 合計 | 回復78% 273/350 (人) | 回復83% 289/350 (人) |
ある薬を飲んだ時にどれくらいの割合で回復するか というデータが上のテーブルである。
何人中何人が回復したかという人数と それをパーセント表示した値が示されている。
男女別にデータがとられているのがミソである。
一見 不思議なことが起きている。
男女とも 薬を飲んだ方が回復率が高い。 つまり この薬は効く様に見える。
しかし最下段 男女合計した人数で見ると なんと薬の効果はネガティブになってしまうのである。
男には効く 女にも効く でも人間には効かない。
そんなことがあり得るんだろうか?
もちろんあり得ない。 データの見方が間違っている。
この薬は男女によって効果に差があり この性質を利用したトリックなのである。
薬は効く。ただし女性の方が男性よりも効きが悪い。
投薬して回復したデータは 効きが悪い女性の方のサンプリング数を増やし
投薬しないで回復したデータでは 逆に減らす。
こうすることで 飲んでも効かなかったというデータの比重をまんまと高めて 合算した時に逆転現象を起こさせているのである。
一番下の「合計」の項で 単純な人数合計のデータを用いて割り算しているのがインチキなのであり パーセントデータの方を用いて平均をとるべきなのである。
人数ちょくではなく 人数で割った”重み付け”のデータを用いるのが吉という事。
男の人数合計は 87+270 = 357
女の人数合計は 263+80 = 343
男女合計で 357+343 = 700
これらで重み付け計算し 男女で偏って取られたデータを平等にする。
薬ありで回復したのは (男93%) x 357/700 + (女73%) x 343/700 = 83.2%
薬なしで回復したのは (男87%) x 357/700 + (女69%) x 343/700 = 78.13%
以上より 人間はこの薬を飲んだ方が回復しやすいと胸を張って言える。
パラドックスはおとろしい。”性別”という要素が伏せられた・それに気づかなかった場合「この薬は人間に効かない」という結論にいい様に誘導されてしまうという事でもあるわけである・・
===
シンプソン問題のそもそもは 算数で常に注意が必要な「加減算と乗除算の混同」のエラーであると言える。
A/B > a/b かつ C/D > c/d
は
✖️ (A+C) / (B+D) > (a+c) / (b+d)
を意味しない。
◯ A/B x C/D > a/b x c/d
こっちが正解。
===
以上は「シンプソンのパラドックス」に対するとりあえずの謎解きであるが
これを因果ダイアグラムで紐解くと こんな感じに見通せてしまう。

性別 薬 回復
”性別”を親としたフォークです。
矢線[a] の存在が 性別によって薬を飲む/飲まないの人数を恣意的に調整した事の白状となっている。
矢線[b] は性別によって効きが違う事を示している。
我々が知りたいのは 薬が効くのか効かないのか。
薬の有無:X=1、X=0 によって 薬の効き:Y=1が出力される割合に どの様な差があるかを 性別という交絡因子に撹乱される事なく求めたいわけであるが
以下 大まかな雰囲気だけの説明になってしまっておりますが・・
まず Xへ入ってくる余計な経路:pa(X)(Xの親:Zのこと)からの矢線[a]を取り除く。
(親(X)は 大きな括りでは”バックドア基準”なるものを満たすノードであり このパスの削除はバックドアパスのブロックという手法)
これでXへのZの影響を遮断した回路となるので この状態でXに0や1を代入する。
(これをXへの”介入”といい do(X=0)、do(X=1) と書いたりする。)
削除した矢線の元親pa(X)に対しては”調整”を行う。
”調整”とは Zによる重み付けを考慮して出力を合計する操作であり すでに述べた「人数の足し算ではなく人数割りのパーセントでデータを見ろ」の計算と全く同じ意味の操作である。
こうして Zで重み付けされたX→Yの因果関係の強度が正しく抽出される。
こういった一連が グラフ読解の過程で機械的に導かれるのが 因果ダイアグラムの威力である。
因果推論を用いない場合は データテーブルをじっと見つめ 頭をひねり パラドックスを見破り 正解に辿り着く という都度都度の力技になる。
恣意的なパラドックスの悪用にも悩まされる・・
因果推論の手法は この工程をアルゴリズム的な作業に落とし込む。
シンプソンの例では ダイアグラムを描く事により 一発でZによる重み付け足し上げという正解にたどり着いた。
===
[ コライダー ]
3つ目の部品 ”コライダー” 。

二つの親が一カ所に合流している。
これが 最も面白い 一見不思議な動作をする。
合流点は 通常は経路をブロックしている。
XY間に因果関係はない 情報が開通していない 両方とも親なので。
しかし Zを条件付けする事により XY間が開通する。
この辺がフォークとは逆の動作であり 一見不思議なのだ。
このあたりが初めは飲み込みずらい。
これが直感と反しているため 人間はパラドックスを感じてしまうのであり
たとえば”モンティホールパラドックス”はまさにコライダーが引き起こしている。
(追:以下コライダーの説明が以前はかなりイマイチでしたので修正しました 2023.6.23)
図のa,bは X,YがZへ及ぼす度合いの係数であり 以下の様な関係を表す(構造方程式と言う)。
Z = aX + bY
a=1,b=2 なら
Z = X + 2Y
さて Zの値がなんだっていい場合は XもYもなんだっていい。
ここからが面白ポイントで
たとえば Z=10 に条件付けされると X,Yは とたんに次の様な相関関係を持つ様になる。
X=2 なら Y=4
X=4 なら Y=3
X=6 なら Y=2 ・・・
反比例のシーソーの様な挙動です。この新たな相関関係を ”擬似相関” という。
才能・美貌・名声 の例。
才能と美貌の間には 基本何の因果関係もない どちらも偶然の贈り物としか言いようのないもの。
例えばハリウッドスターとしての名声が これらを親とした因果関係にあるとすると グラフはこの様になるだろう。

A才能 C美貌 B名声
才能があり余っている場合にはイケメンである必要はない。
美貌に光り輝きまくっている場合には才能は大目に見られるかもしれない。
才能がそこそこならそこそこイケメンである必要がある。
名声がそこそこで良いのであれば 才能と美貌のハードルも全体的に下がっていく。
そして両方とも無いとなるとエンタメの世界で生きていくのは厳しいだろう・・
合流点”名声”の値を条件付けすると 才能と美貌の間にはこの様な”擬似相関”が生じるのだ。(例え雑すぎ怒らないで・・)
コライダーでは
Bが自由な限り AとCの間に相関はない。 AC間の相関関係はBによってブロックされる。
ところが Bの値が固定される:”条件付け”されると AとCの取り得る値に相関関係が発生する:AC間に情報伝達経路が開く!
コライダーはダイアグラムの中でこの様な論理素子として動作する。
===
モンティホール問題のダイアグラムは この様な形になる
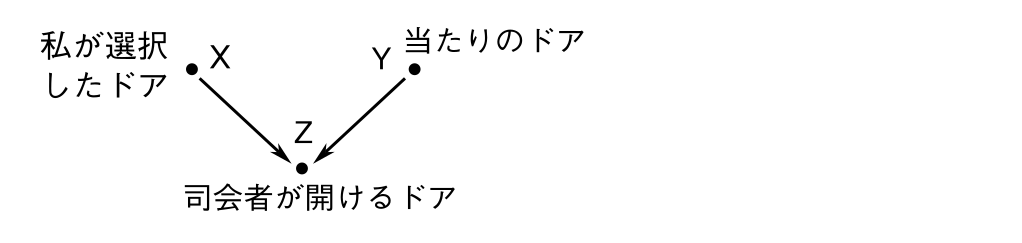
X私の選択したドア Yお宝のあるドア Z司会者が開けるドア
コライダーになっている。
司会者が何もしない限り 私の選択したドアと お宝のあるドアとの間には 何の相関関係もない。 確率は1/3のランダムである。
しかし 司会者がドアを開ける:つまり合流点Zの値を条件付けしたとたん X:私の選択したドア と Y:お宝のあるドア の間に擬似相関が生じる。
司会者は 当てずっぽうの確率1/3でドアを開けているのではない。
XとYそれぞれから情報を受け取る合流点として 両者を参照し その限定された条件下で開けるドアを選んでいるのだ。
X私が選んだドアでは無く Yお宝があるドアでもない ドアZを。
そのとたん XとYの間に相関関係が生じる。
X私が選んだドアでは無く Z司会者が開けたドアでもないドアが Yお宝があるドアである可能性が高い という相関関係である。
合流点Zの条件付けが 矢線で直接結ばれていないXとYの間に相関関係を開通させる などという事が 人間の脳にはなかなか飲み込めない。
あたかも因果関係の矢の方向とは逆方向の作用が動作しているかに見えるのも ぱっと見では奇妙だ。
この感覚がパラドックスなのだ。
この発見は 噛めば噛むほど面白い 驚いてしまう。
===
以上 因果ダイヤグラムの構成部品である3つのパーツの 簡単なご紹介でした。
どんな構成のダイヤグラムも この3つのパーツの組み合わせで作り上げられる。
そして それぞれのパーツの動作はわかっているのであるから
その集合体である大きなダイヤグラムも分解して読み解くことができ
知りたい因果関係X→Yに正しくフォーカスすることが可能となるのである。
===
[ 反事実 ]
さて ここまで来ると 完成した因果回路を用いて ”反事実”を予測することが可能となってくる。
システム全体の構成・パラメータは当時と変えず 一箇所だけ事実とは異なるデータをセットする。
再現不能な状況 現実には起こらなかった「もしあの時こうしていたら こうなったはずだった」の状況を作り出す。
こんな事が可能なのは 因果ダイアグラムという世界モデルが手元に完成しているからである。
あとは 自由な非現実的な初期値に対し システムを動作させ 予言的出力を得ることができるわけである。
(テキストでは「反事実」という用語が強調されますが 私は要するにシミュレーションの事だと思うのですが 雑な理解だろうか・・)
これはまさに 因果関係を推測し もしもの並行世界を想像したり もしもの未来に備えたりする 人間の脳がやっている事ではないでしょうか?
そして 今のところAIにはごっそり欠けている能力なのかもしれない・・
==================================
さて これ以上は教科書を読んでいただくのが一番よい どう考えても。
私もそろそろ 無責任な聞き齧り説明をこれ以上続けるピエロな羞恥心と疲労が限界であります(そもそもが自分の頭を整理したいメモみたいなものから始まっており)。
最後に ここまでのまとめ的な意味と ちゃんと勉強したい場合への予告編的概略として:
因果推論という技術の手順は要するに大まかにはこんな感じ?
・因果ダイヤグラムを書いてみる:図面を引く:仮説モデルを作る
(構造方程式の連立方程式という表現方法もある)
・ダイアグラムの構造を読み解き グラフ操作テクニックを駆使し
今回知りたい因果関係(X→Y)に関する確率の式を導き出す。
これは ”介入” do(X=x)〜 とか ”反事実” Yx=1〜 とかいった 因果推論独特の作法で記述されます。
・これらに対し「調整化公式」などなどを使い 重み付けなどなどの解釈を行い
いわゆる Σ𝑃(𝐵|𝐴)P(Z)〜 みたいな 情報統計的な式・数学の式に翻訳する。コンピュータが読める形にする。
・こうしてできたプログラムにデータを流し 欲しかった結果:因果関係X→Yを得る。
将来人工知能に組み込まれるかもしれない「因果推論エンジン」は
結果の評価・実測データとの食い違いの評価を モデルの修正にフィードバックし 精度を上げ 〜 のループを回し 現実を反映したダイヤグラムに辿り着こうとする
・・みたいな構成なのかな。
こういったアルゴリズムは まさにコンピュータの得意分野である。
人間は ここまで述べた様に 因果推論の中に苦手な部分があり 往々にしてパラドックスに陥る。
コンピュータはそんな間違いは犯さない。 誰が犯人か 誤謬なく論理的に推論することになる。
AIが 「こんなことになってるのは 全てあいつの仕業です。」とか言い始めるその日 世界は次の段階に入るのかもしれない。
===
[ あるいは・・・ ]
ChatGPT 本当に何かが創発しているのか?
僕個人は今回の読書を通して 人間の脳が因果関係の解釈にいろいろとミスを犯すこと パラドックスを感じてしまうことを学びました。
するとですね
人間は データ統計の化け物であるにすぎない者・機械的な情報操作による入出力結果に対して その評価にミスを犯す:”神秘”を感じてしまう可能性に思い至るわけです。
AIが人間の脳に近づいた
という可能性と
人間の脳はAIを自分の仲間だと勘違いしてしまうアホの子だ
という可能性は
パラレルかもしれん あるいは相互参照かもしれん・・
2023.6.18
=================================
*1)
大変興味深かったのですが 理解に苦労した部分もすごく多く
というのもこの本は啓蒙書的読み物で 教科書としての機能はいまいち弱く
きちんと理解するためにはどうしても教科書を読まねばならん・・
という事で

「入門 統計的因果推論」Judea pearl / Madelyn Glymour / Nicholas P.Jewell
同じ先生が書いた教科書。
コンパクトな入門書的教科書で わからなかった所がかなりクリアになってきた・・ のですが
翻訳教科書である事のあるあるで「果たして私はちゃんと内容を汲み取れてるのか いろいろ誤解誤読してないか 翻訳は大丈夫なのか」みたいな自分勝手な不安に苛まれ それではということで今度は 日本語の先生が書かれた本に手を出す羽目になっていき
「構造的因果モデルの基礎」黒木学
この教科書をところどころかじる過程で 先のパール先生の教科書に対する引っかかり点が解消していき そもそもそれが初めから素晴らしい入門書であったことを遅ればせながら思い知り 最初に読み取れなかった私の理解力の問題であった事を思い知る。
学生あるあるの教科書放浪記。 このじじいめにはこの感じは誠にひさしぶりな感覚じゃった。
===
*2)
番組では
「タイムラグが考慮されているので 因果関係の方向についても分析対象になっている」的な脚注が一瞬入りました。
確かに 時系列を見ているのであれば因果関係を捉えられる。
しかし すぐに思いつく不安点として「ニワトリとタマゴ問題」が浮かぶ。
サンプリング範囲の問題である。
データをいつどのぐらいの期間集めたかで 原因と結果は容易に混乱する。
振動現象は宇宙の基本的運動なので こんなことはしょっちゅう起こるであろう。
番組の最後の総括では 出演者の方々が
「因果関係はデータを読む側で推察し考えていかねばならない」
的な締めで終わった。
「データを解釈するのはあくまで我々人間の役目。より良い社会のためデータを活用していきましょー。それではさようなら。」
翻訳すれば
ビッグデータは相関関係を担当
人間の脳は因果関係を担当
です。
===
*3)
物理量と計器の例は ”アイス”の例よりさらに単純な例に見えますが 深遠な真理が隠れている。
「科学の道具である数式は因果関係を記述する機能を持っていない」というそもそも論である。
気圧計の値B 大気圧P として
B = kP
この記述は コンピュータのプログラム の世界では
「Pに値を代入することによりBに値がセットされる」を意味し
確かに因果関係 P→B 的な意味合いを持つ。
大気圧が気圧計の値を上下する。
が これが物理数学的な関係式である場合 その様な因果関係は内蔵されない。
変形して
P = 1/k・B
とすることによって因果関係が B→P に逆転するのだろうか?。そんなことがあるはずがない。
つまりそもそも B=kP に因果関係の概念は含まれない。
数式は相関関係しか語らないのだ。
この事実の中に 科学は因果すなわち時間の矢をうまく語れない という事の根本が内蔵されている事に気づかされ ふいをつかれびっくりする。
確かに・・科学は”時間”が流れているということの取り扱いに四苦八苦している。
エントロピー(不等式による左辺と右辺の非対称)にすがったり 「時間などない!」と言い出すしまつ・・パニクるなっ!
・・わたくしの素人哲学はこのくらいとさせていただきます。
=================================
