１. 確率を目で見る

　確率の視覚化に関しては、それほど語る内容は多くありません、今のところ。
ゆくゆくは、もう少し内容を膨らませられればとは思ってます・・

　さて、サイコロの中の特定の目、例えば１が出る確率は１／６ですが、それを、６mmの長さの中における幅１mm、というかたちでイメージ化します。
基本単位mmを使って、なんとか分のなんとかという抽象概念を視覚化できる物に置き換えて、スケール感をつかみ易いようにしているのです。
それでは、最後の話題として、当選確率１千万分の１レベルと言われる宝くじについて調べてみます。
宝くじの一等というものに対するするイメージはどんな感じでしょうか。
相当厳しそうな印象ではあるが、もしかしたらそこそこ運が良ければ私にも万が一的なチャンスがあり得る物なのでしょうか。
たぶんあると信じているからの人気だとは思われます。

まずは切りのよい値の確率について順番にみると、

確率１／１０：1mm/10mm　すなわち１mm／１cm
確率１／１００：1mm/100mm　すなわち１mm／１０cm
確率１／１０００：1mm/1,000mm　すなわち１mm／１m
確率１／１万：1mm/10,000mm　すなわち１mm／１０m
確率１／１０万：1mm/100,000mm　すなわち１mm／１００m

まだまだどんどん行けますが、この辺りでとりあえず止めておきます。
１００mというサイズに到達しました。
１０万分の１の確率は、長さ１００mの中の幅１mm、と読んでください。

抽選のイメージっぽくするために、ルーレットやダーツのまとの様に円形にしてみます。
円周率3.14で割り算するだけなのですが。

確率１／１０　は、直径３.１８mm の円盤の中の幅１mm
確率１／１００　は、直径３.１８cm の円盤の中の幅１mm
確率１／１０００　は、直径３１.８cm の円盤の中の幅１mm
確率１／１万　は、直径３.１８m の円盤の中の幅１mm
確率１／１０万　は、直径３１.８m の円盤の中の幅１mm

上記した”幅1mm”というのは、円周の部分が幅1mmの細長い三角形：極細のピザの切れ端のようなかたち的な物ですね。
あなたの投げた矢が直径３１.８cmの円盤の中の幅１mmのエリアに命中したとき、確率千分の１に当選という感じです。
確率１／１０、１／１００、１／１０００それぞれを図にしてみました。

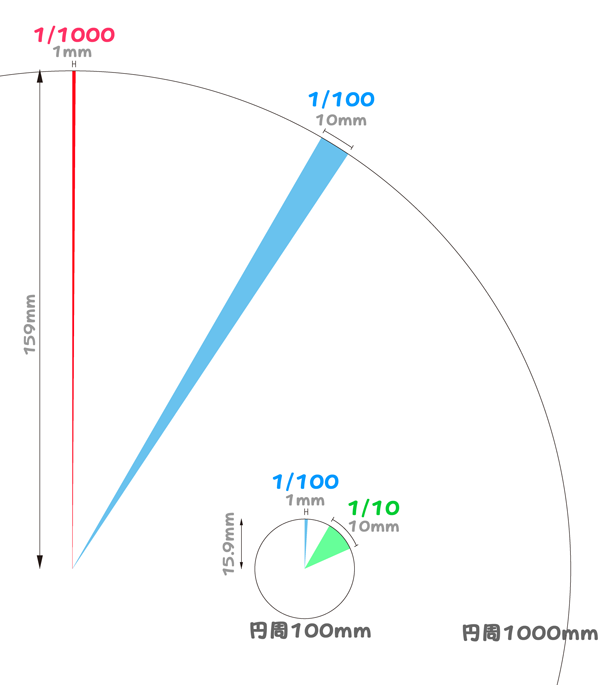
実物大画像ファイル(300dpi Ａ４プリント用)はこちら>>

歩いたり手に取って眺めたりで実感する事がスケールの把握にとって有効、というセオリーが今回も当てはまるのではと思っています。
若干意外かもしれませんが、確率１／１０００あたりでもうすでに、ほとんど無理な印象の確率であると視覚的に理解されます・・

　では、当選１千万分の１のレベルと言われる”宝くじ”の当たる確率を。
確率１／１千万：1mm/10,000,000mm　すなわち 1mm/10km
10km を円形にすると、直径 3.18km となります。

私の感想を言えば、正直やっぱり今回も「びっくりした」です。
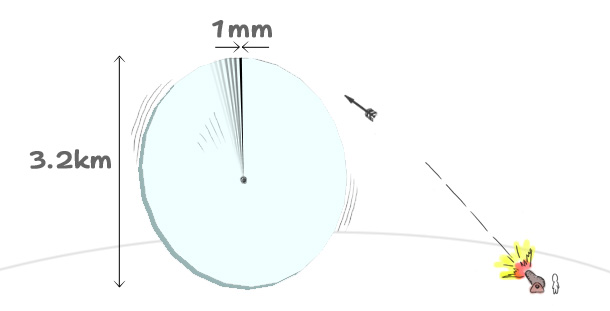
直径3.2kmの回転円盤に向けて発射された矢が（もはや人力では無理でしょう）幅1mmの回転するスリットに命中する確率、それが１千万分の１と判明しました。
ちなみにこの円盤の円周１０kmは徒歩で回ると２時間半です、と咄嗟に計算するのはもう病気かもしれません・・

さて、これで本当におしまいです！

なにか１つでも面白いと感じていただけた事、センスオブワンダーがあったとしたら、望外の喜びであります。