付録１．基本的な方針

このサイトで扱っているのは、次のような種類の数についてです。

・距離、長さ
・時間
・数

それぞれ、普通使われている単位は

・メートル、キロメートル、光年・・・
・時、日、年・・・
・人、枚、本・・・

等さまざまですが、私がこだわっているのは体感的、身体的、皮膚感覚的な把握という事です。
そこでまずは、すべての人が身体感覚として自然にイメージでき、確実に把握できる長さ、時間、数の物差しの基準、最小単位をおおまかに設定し、考えを進める出発点にしてみることにしました。

１．距離

　まず距離や長さについてですが、たいがいの人が肉眼で無理なく見分けられ、長さとして実感できる一番小さな大きさは、１mmというサイズではないかと思います。
１mmと聞けば、ほとんどすべての人はその長さ、小ささの程度をイメージでき、実感できるのではないでしょうか。
アリの大きさが３mm、ぶどう一粒の大きさが１０mm、と言われればだいたい正確にイメージできるのではないでしょうか。
それに、手元に定規があれば、いつでもすぐ肉眼でその大きさを確認することができます。
このような事から、大きさの最小基本単位は１mmと置きます。

長さについてはもう一つ別の目盛り、すごく長い距離をイメージするためのものとして、歩行速度を採用したいと思います。
歩行という行為は自分の体を使って日々体験する事ですので、距離感、速度感の基準として何よりも有効です。
ただ、歩く速さは人それぞれ若干ばらつきがあるかもしれません。
不動産広告でよく見る徒歩何分、あれはだいたい時速５km弱くらいだという事らしいですね。
広告独特の数値感覚を考慮し、また子供や女性も含めたおおまかなアベレージを想像して、時速４kmくらいを使用するのが妥当かなと思っています。
以下ではこの値を用いていきますが、あなたご自身の歩行速度を使っていろいろな数値を計算し直すと楽しいかもしれません。

ここで念のため mm、徒歩の両者の関係を確認しておきます。徒歩速度 4km/時 として、
4km/時 = 4000m/時 = 66.66m/分 = 1.111m/秒 = 1111mm/秒
です。

２．時間

　長さの基準を考えたときと同じ要領で、身体感覚としての時間の最小単位を考えてみると、やはりそれは"１秒"ではないでしょうか。
１秒２秒という感覚は私たちにとってとてもなじみ深い時間感覚ですし、かつ分解できる最小の単位だと思います。
また、手近の時計の秒針などで、秒間隔の感じはすぐに確認できるでしょう。
ただ、長い距離を扱う場合にmmでなく徒歩スピードを用いる事にしたように、時間についても場合に応じて、時、日、年、という単位を使うほうが便利です。
これらの単位の時間の長さの感じは、秒に対する感覚とはちょっと質が異なるような気もしますが、それぞれどれも私たちの皮膚感覚として実感が可能な単位ではないかと思います。
また既に、徒歩速度を考える場面で時速という単位を使用しております。
時間に関しては少々混乱気味のような気もしますが、やはり”時間”は難しいのであります・・
時間に関するぼやけたイメージをクリアにするために用いる「単位の置き換え操作」については後ほど述べます。
さて、秒と時、日、年の相互関係を確認しておきます。

1時間 = 1,600秒
1日 = 86,４00秒
1年(365.25日として) = 31,557,600秒

この 31,557,600秒 という大きな数に関しては「単位の置き換え操作」の項で再調査します。

３．数

　数すなわち個数というものの大きさについてです。
個数の計り方の基本は、当たり前すぎるかもしれませんが自然数です。
１、２、３、と自然に物を計っていく数値が自然数ですが、もちろん人間にとってとても自然な事です。
最小単位はむろん"１個"という事になります。
もっと具体的に言えば、１個という場合、１粒の玉のイメージです。
ただし、私がそもそも問題にしているのは、簡単には実感できないばかでかい数、何十万とか何億とかいった自然数を感じる方法です。
そして”１万個とは１万粒の玉だ”という記述は、このままでは無意味であります。
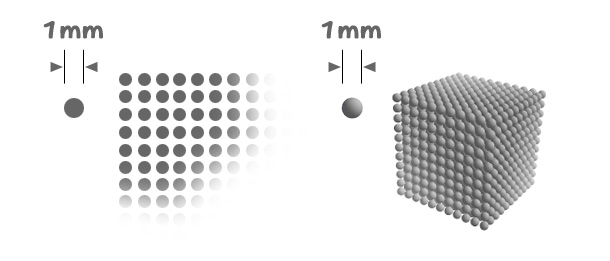
そこで、大きさの最小単位として決めた mm と言う基準体感スケールを、数を数えるという場合にも適用する、という事をやります。
”１つ”という数のイメージの最小単位を直径1mmサイズの丸い点、あるいは直径1mmサイズの球の粒である、とイメージします。
一列に並んだ点、平面に整列した点、はたまた球のつぶつぶが立体的にぎっしりつまって整列しているイメージです。
個数をmmという長さの基本単位に結びつけるやりかたが「単位の置き換え」です。

４．確率

　確率は、時間や距離の様に物差し的なイメージの数値とはちょっと毛色が違うような感じもしますが、長さの基本単位を元にイメージ化ができます。
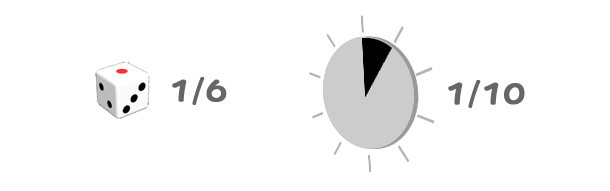
確率と言えばまずはサイコロですが、６分の１という確率は最もなじみ深い確率かも知れません。
確率１／６の感触がわかれば、同じようにして１／１０、１／１００ と、イメージを広げていける様な気がします。
たぶん１０、１００という自然数がまだくっきりとイメージできる射程内にあるからではないかと思います。
では千分の１の確率で当たる抽選会、これはイメージできるでしょうか？
この辺りからかなりおぼつかなくなってくるのではないでしょうか。
ここで、自然数 1,000個 を 1,000mm すなわち １m に置き替えてみます。
１m のラインの中の 1mm の幅、それが確率１／１０００です。
抽選会ですので、直線ではなく丸いダーツ盤にしてみましょう。
円周１mの円の直径は31.8cm。
その円盤に幅1mmの三角形（極細のピザの切れ端のようなかたち的な物のイメージ的な物を想像されよ）が刻まれています。
あなたの投げた矢が見事その厳しいエリアに命中したとき、確率1/1000獲得です。